Skip to content
Home » Three ways to calculate the RSI in Python

Three ways to calculate the RSI in Python

Tags:

One of the most widely used technical indicators in technical analysis is the Relative Strength Index. It measures the magnitude of recent price evolutions to evaluate if a price of an asset is overbought or oversold. In this blog post, I list the many ways you can calculate the RSI in Python.

🤓 Like stochastics, MACD, and ROC, RSI belongs to a group “loosely referred to as oscillators […] While the arcane names and imposing formulas of many oscillators may initially seem confusing, virtually all of these indicators are based on the concept of momentum, which, not surprisingly, refers to the rate (or speed) at which prices change.” Jack D. Schwager in Getting Started in Technical Analysis

The RSI was introduced by Welles Wilder Jr. in his 1978 book New Concepts in Technical Trading. However, there is no such thing as the relative strength index. There are many ways to calculate it. For each piece of code below, I’ll also discuss the methodological choices.

Calculate the RSI using nothing but Pandas

In the following code chunk, there is a function that you can use to calculate RSI, using nothing but plain Python and pandas. You pass the function a DataFrame, the number of periods you want the RSI to be based on and if you’d like to use the simple moving average (SMA) or the exponential moving average (EMA). By default, it uses the EMA.

import pandas

def rsi(df, periods = 14, ema = True):
    """
    Returns a pd.Series with the relative strength index.
    """
    close_delta = df['close'].diff()

    # Make two series: one for lower closes and one for higher closes
    up = close_delta.clip(lower=0)
    down = -1 * close_delta.clip(upper=0)
    
    if ema == True:
	    # Use exponential moving average
        ma_up = up.ewm(com = periods - 1, adjust=True, min_periods = periods).mean()
        ma_down = down.ewm(com = periods - 1, adjust=True, min_periods = periods).mean()
    else:
        # Use simple moving average
        ma_up = up.rolling(window = periods, adjust=False).mean()
        ma_down = down.rolling(window = periods, adjust=False).mean()
        
    rsi = ma_up / ma_down
    rsi = 100 - (100/(1 + rsi))
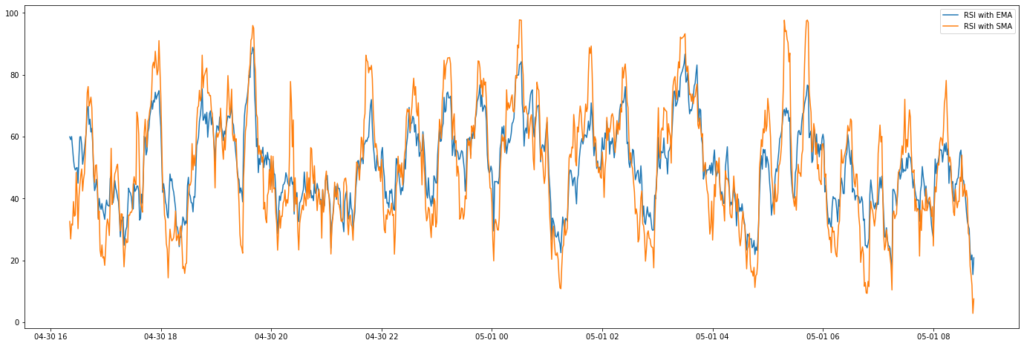
    return rsi

Visualized below is the difference in sensitivity between the RSI calculated with the EMA and the RSI calculated with the SMA. As you can see, there are more extremes if you use the SMA variant.

RSI in Python using plain Python

👀 Things to note regarding the ewm method:

  • It is important that you use the min_periods parameter in the ewm method, in order not to calculate an RSI in the first periods of your time series, that is based on incomplete data.
  • If you set the adjust parameter to True, a decaying adjustment factor will be used in the beginning of your time series. From the documentation: “Divide by decaying adjustment factor in beginning periods to account for imbalance in relative weightings (viewing EWMA as a moving average).

Calculate RSI using the TA-lib Python wrapper

✌ Installing TA-lib for Python can be somewhat of a nuisance, so please follow short my tutorial, especially if you use a custom notebook solution like Deepnote.

If you’re a fan of the widely used TA-lib library: good news! TA-lib supports the RSI out of the box. 

import talib as ta

ta.RSI(df['close'], timeperiod=14)

TA-lib uses the same exponential moving average function as our custom function described earlier in this article. However, the first time it is calculated for a time series, it uses a simple moving average. That’s why it differs slightly at the beginning of our time series.

Calculate RSI using the pandas-ta library

Another convenient package for technical analysis in Python is pandas-ta. Just like TA-lib, it uses an EMA version. However, here too, in the beginning of the time series, it differs from the initial function provided in this article. That’s because it uses Wilder’s Moving Average.

import pandas_ta as pta

pta.rsi(df['close'], length = 14)

It comes with extra parameters such as:

  • scalar: multiply the RSI by a specific scalar — maybe you like base 1000 or 1?
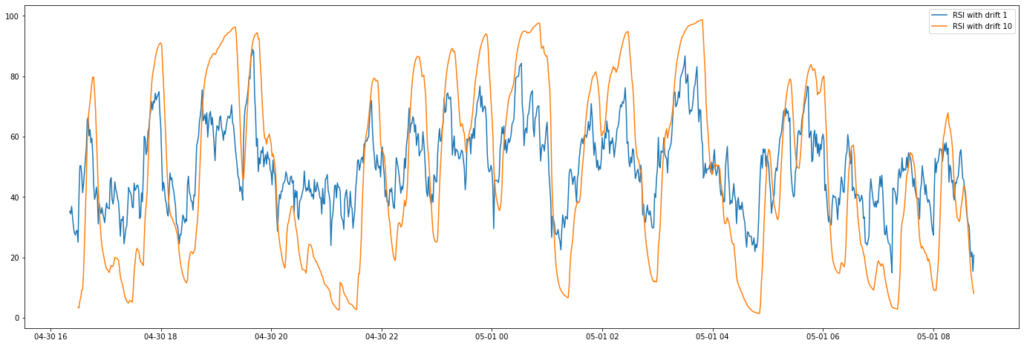
  • drift: instead of using the difference in closing price at each period (drift = 1), you can use the difference in closing price between periods over a longer time period. In the example below, I compare pandas-ta’s RSI with drift set to 1 and 10.
RSI in Python using pandas-ta

Great success!

Say thanks, ask questions or give feedback

Technologies get updated, syntax changes and honestly… I make mistakes too. If something is incorrect, incomplete or doesn’t work, let me know in the comments below and help thousands of visitors.

108 thoughts on “Three ways to calculate the RSI in Python”

    1. Ggcool

      df[“price_change”] = df[“close”] – df[“open”]
      df[“up_move”] = df[“price_change”].apply(lambda x: x if x > 0 else 0)
      df[“down_move”] = df[“price_change”].apply(lambda x: abs(x) if x < 0 else 0)
      df["avg_up"] = df["up_move"].ewm(span=27).mean()
      df["avg_down"] = df["down_move"].ewm(span=27).mean()
      df["RS"] = df["avg_up"]/df["avg_down"]
      df["RSI"] = df["RS"].apply(lambda x: 100-(100/(x+1)))

      Reply
  5. RedRaven

    Good article. There’s a small mistake in the first function in the if statement there should be a double equal sign. (if ema == True:)

    Thanks for sharing!

    Reply
  11. john

    Million dollar question, which is fastest, best, most reliable etc? I can’t get ta-lib to build a wheel on my Windows 10 machine with Python 311, so my choice is between the Python or Panda_ta version above. Thoughts? Thanks!

    Reply
  19. slot303

    Heya i’m for the first time here. I came across this board and I find It truly useful & it helped
    me out much. I hope to give something back and help others like you aided me.

    Reply
  22. bbw

    Hi my loved one! I want to say that this post is
    awesome, great written and come with approximately all significant infos.

    I’d like to peer extra posts like this .

    Reply
  24. myfriv

    Everything is very open with a clear clarification of
    the challenges. It was truly informative. Your website
    is very helpful. Thanks for sharing!

    Reply
  39. quay thu mb

    quay thu mb là địa chỉ quay thử xổ số miền Bắc có xác suất cao nhất hiện nay. Những con số may mắn đang chờ bạn, hãy thử vận may ngat cùng quaythumienbac.com #quaythumienbac #quaythuxosomienbac #quaythumienbaccom

    Reply
  69. slot gacor hari ini

    Hey there are using WordPress for your site platform?
    I’m new to the blog world but I’m trying to get started and set up my own. Do you
    need any html coding expertise to make your own blog? Any help would
    be greatly appreciated!

    Reply
  72. slot 2d

    SLOT2D merupakan Situs Slot Minimal Deposit 5000 Via Dana dengan Daftar
    Game Judi Slot Deposit Pakai Pulsa Indosat 5000 dan menyediakan pola slot pragmatic bet
    murah terbaik.

    Reply
  73. Etta

    Etta will gather and compile a comprehensive collection of high-quality links, ensuring you have access to all the information and resources you need. This way, you’ll have a well-rounded and reliable source to refer to, making your research or task much easier. Let’s dive in and get started!

    Reply
  99. singapore sushi

    Pretty great post. I simply stumbled upon your blog and wanted to say that I have truly loved
    browsing your weblog posts. After all I’ll be subscribing on your feed and I’m
    hoping you write once more very soon!

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

Related Posts

How to do a SUMIF in PySpark

  • by
  • 2 min read

One of the most frequent used Excel functions is probably SUMIF and its SUMIFS variant. In this article, you’ll learn how to do exactly the… 

Read More »How to do a SUMIF in PySpark

Check if Python logger already exists

I recently got more interested in observability, logging, data quality, etc. For many use cases, you don’t need full-blown observability solutions. Python has robust tools… 

Read More »Check if Python logger already exists

Spark 3.0: Solving the “dates before 1582-10-15 or timestamps before 1900-01-01T00:00:00Z” error

In the past couple of weeks, I’ve been working on a project which users Spark pools in Azure Synapse. However, this appears to be a… 

Read More »Spark 3.0: Solving the “dates before 1582-10-15 or timestamps before 1900-01-01T00:00:00Z” error