R: Is a bootstrap of mean differences statistically significant

Last year, I wrote a blog post about bootstrapping (two-sample) the mean in R. Recently, someone contacted me with the question of how to get the corresponding percentile for a specific value of those bootstrapped differences. It’s something you need to answer the question if the difference is statistically significant from 0. Let’s do it in this blog post.

In the previous blog post, I stored my 2500 bootstrapped differences in a vector. Let’s call it mean_diffs. If we want to get a percentile for a specific value, we need to produce a cumulative distribution first. We can do this using the ecdf function, which produces a cumulative distribution function from the values we provide it.

We provide ecdf() with the vector and we plot the resulting function.

cdf <- ecdf(mean_diffs)
plot(cdf)

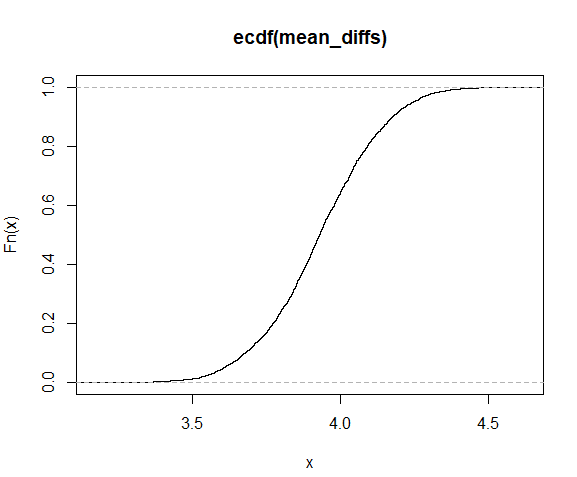
The object cdf is a function. We can provide it with a value and a corresponding percentile will be returned. For example, if we’d like to check if our mean differences are statistically significant from zero, you can provide the function a zero.

cdf(0)

In our example, the corresponding percentile is 0. However, if the difference between both samples is less obvious, it won’t be zero.

Finally, not only can you plot the function or have it return a value, you can also ask for a summary.

summary(cdf)

Like this:

In this blog post you learned how to determine if the bootstrapped difference is statistically significant from zero.

By the way, if you’re having trouble understanding some of the code and concepts, I can highly recommend “An Introduction to Statistical Learning: with Applications in R”, which is the must-have data science bible. If you simply need an introduction into R, and less into the Data Science part, I can absolutely recommend this book by Richard Cotton. Hope it helps!